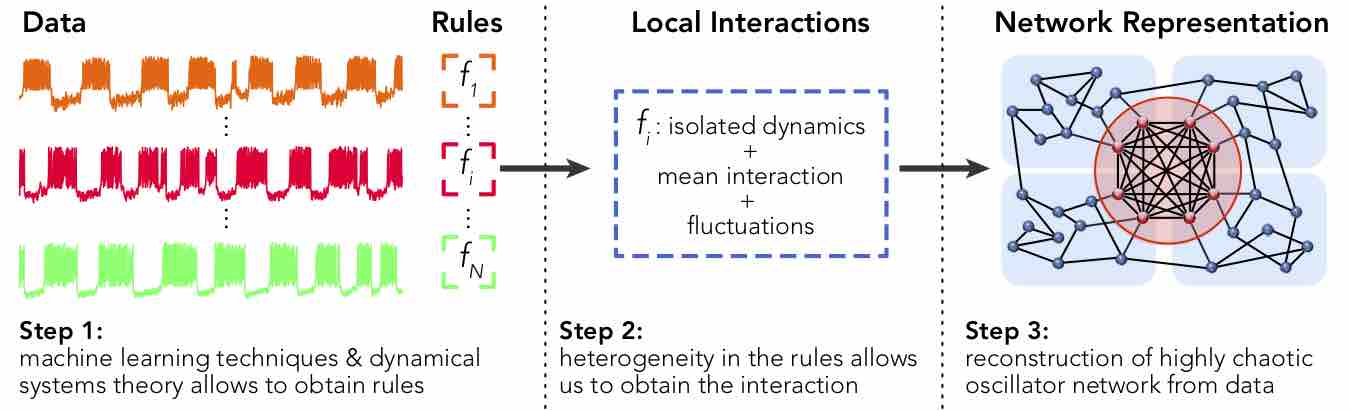
Real-world complex systems such as ecological communities and neuron networks are essential parts of our everyday lives. These systems are composed of units which interact through intricate networks. The ability to predict sudden changes in network behaviour, known as critical transitions, from data is important to avert disastrous consequences of major disruptions. Predicting such changes is a major challenge as it requires forecasting the behaviour for parameter ranges for which no data on the system is available. In this paper, we address this issue for networks with weak individual interactions and chaotic local dynamics. We do this by building a model network, termed an effective network, consisting of the underlying local dynamics at each node and a statistical description of their interactions. We illustrate this approach by reconstructing the dynamics and structure of realistic neuronal interaction networks of the cat cerebral cortex. We reconstruct the community structure by analysing the stochastic fluctuations generated by the network and predict critical transitions for coupling parameters outside the observed range.